Skip to main content Link Search Menu Expand Document (external link)
Wearable BP

Here, we provide details of and insight from the measure used in our paper, Explained Deviation (ED).

Explained Deviation

To account for heterogeneity in calibration technique and BP distribution between studies, introduce a measure called “Explained Deviation” or \(ED\), which normalizes the errors by the BP distribution.

\(ED = \frac{\sigma_{pop}}{\sigma_{pop, \epsilon}}\) for subject split studies

and

\(ED = \frac{\sigma_{\Delta}}{\sigma_{\Delta, \epsilon}}\) for personalization studies

where:

\(\sigma_{pop}\) is the standard deviation of the BP distribution of the whole dataset

\(\sigma_{pop, \epsilon}\) is the standard deviation of the BP estimation errors of the whole dataset

\(\sigma_{\Delta}\) is the standard deviation of the change in BP distribution of the whole dataset

\(\sigma_{\Delta, \epsilon}\) is the standard deviation of the change in BP estimation errors of the whole dataset

We show several motivating cases:

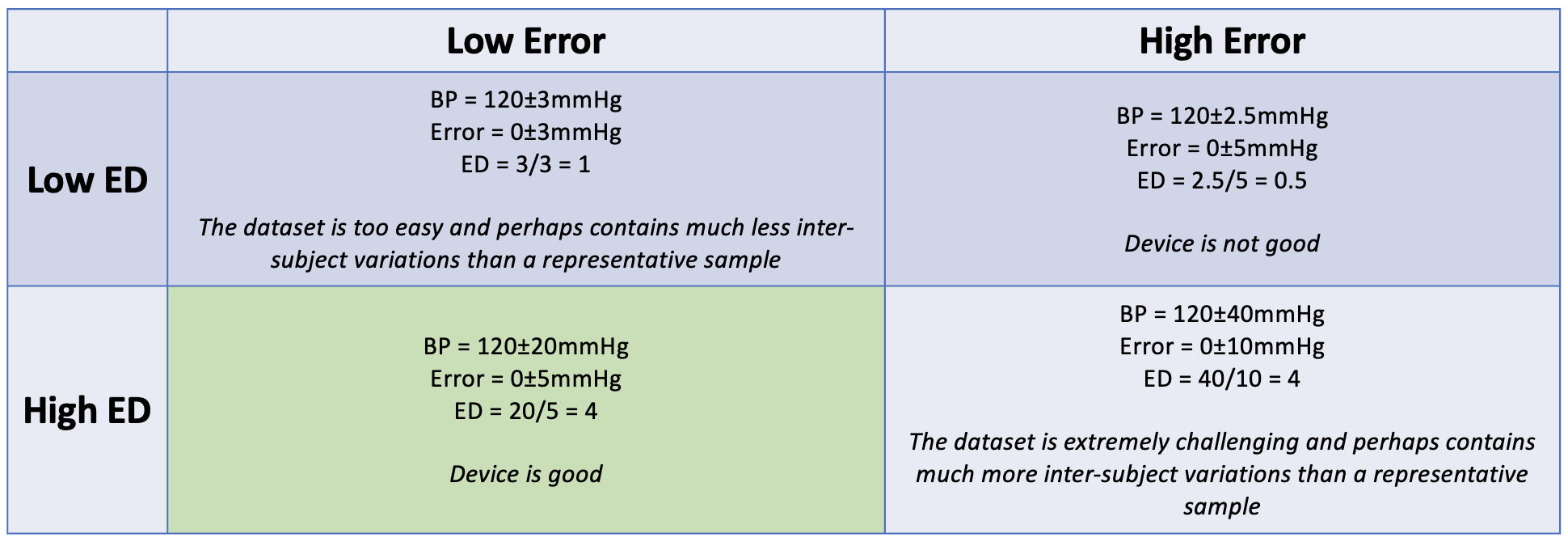
We can compute confidence intervals and perform hypothesis testing since ED is related to the F-distribution. We also compute \(ED_{min}\), the estimated minimum ED required to meet the AAMI/ANSI/ISO 81060-2:2019 standards. \(ED_{min}\) for SBP and DBP were 2.17 and 1.39.

Next we report several insights:

Distribution of SBP and DBP Explained Deviations: SBP has larger proportion of studies that have higher Explained Deviation.

<!DOCTYPE html>

Bokeh Plot

<!DOCTYPE html>

Bokeh Plot

How DBP Explained Deviation varies with SBP Explained Deviation

We plot the ED of SBP versus ED of DBP for subject split and personalization studies. The size of the points are inversely proportional to the marigin of error. We delineate in green the minimum ED (\(ED_{min}\)). Notice that even though many studies report low error, they have an ED of around 1.

<!DOCTYPE html>

Bokeh Plot

Appendix 1: Explained Deviation Confidence Interval

Assume:

  1. \(n_1\) independent samples from a normally distributed population with variance \(\sigma_1^2\)
  2. \(n_2\) independent samples from a normally distributed population with variance \(\sigma_2^2\)

Given sample variance \(s_1^2\) and \(s_2^2\), we can write \(\frac{(n_1 - 1)s_1^2}{\sigma_1} \sim \chi_{n_1-1}^2\) and \(\frac{(n_2 - 1)s_2^2}{\sigma_2} \sim \chi_{n_2-1}^2\) The ratio of these two distributions is an F-distribution and can be written in the form:

\[F~\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}\]

The \(1-\alpha\) confidence interval can be written as:

\[P(F_{\alpha/2}(n_1-1, n_2-1) \leq \frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2} \leq F_{1-\alpha/2}(n_1-1, n_2-1)) = 1-\alpha\]

Substituting \(\frac{s_1}{s_2}=ED_{est}\), \(\frac{\sigma_1}{\sigma_2}=ED_{true}\), and \(n_1=n_2=n\) gives:

\[P(\sqrt{F_{1-\alpha/2}(n-1, n-1)} ED_{est} \leq ED_{true} \leq \sqrt{F_{\alpha/2}(n-1, n-1)} ED_{est}) = 1-\alpha\]

Appendix 2: Estimating required Explained Deviation from AAMI/ANSI/ISO 81060-2:2019

The AAMI/ANSI/ISO Standard specifies that a device that for the general population should:

  • Have n=85 subjects, should include ≥30% males and ≥30% females
  • Have ≥5% of the reference SBP readings ≤100 mm Hg, ≥5% with ≥160 mmHg, and ≥20% with ≥140 mmHg
  • Have ≥5% of reference DBP readings ≤60 mmHg, ≥5% with ≥100 mmHg, and ≥20% with ≥85 mm Hg

We used subsamples of a current publicly available dataset that satisfies these demographics (PPG-BP). To determine a subsample that satisfied the AAMI/ANSI/ISO Standards, we performed weighted sampling of subjects, where the weights were determined using Iterative Proportional Fitting (IPF) marginalized on the requirements. We repeated this process 10000 times and determine the minimum variance of the subsampled datasets. Then, we took the maximum error standard deviation allowed by AAMI/ANSI/ISO (±8mmHg). The minimum ED for SBP and DBP was computed to be 2.17 and 1.39. The implementation can be found on Github.